Taking a look at flying tricycles versus taildraggers.
After learning to fly and exploring Utah for five years in a little tricycle-wheeled putt-putt Piper Cherokee, this year I decided to expand my skills and capabilities with a back-country worthy taildragger. There was lots of ominous hangar talk (“you will ground loop this plane“) as well as the FAA‘s requirement that you not merely land the plane three times in three months but bring it to a full stop if you want to carry passengers. This led me to the impression that there’s something inherently unstable about these backward aircraft.

Figure 1: The antagonist of my ground-loop nightmares.
Last week, as part of my day job, I was explaining the concept of center-of-mass to a group of college students. It occurred to me that center-of-mass is key to understanding the tailwheel’s instability. The location of the center-of-mass relative to the fixed and turnable wheels on an aircraft determines the relative stability (in the case of tricycles) or instability (in the case of taildraggers) of the plane one is trying to take off or land.
Mathematically, the center-of-mass is the average location of the mass of an object. And according to Isaac Newton’s laws of motion, any extended object behaves as a pointlike object located at the position of the center-of-mass. The center-of-mass of an airplane which is moving parallel to a runway centerline will want to continue to move parallel to that centerline. This is a consequence of Newton’s First Law of Motion:
An object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force.
It turns out that this tendency (also called inertia) of the center-of-mass to continue “with the same speed and in the same direction” is what accounts for the relative stability of tricycle-geared aircraft when compared to taildraggers.
Physicists like to model complex objects as simple shapes for the purpose of calculation. A sphere is best, but that’s a little too simplified for what we’re trying to explain about airplanes. So we’ll use a triangle, with wheels at the corners. Consider the representation below (Figure 2) of a tricycle-geared airplane lined up with and moving parallel to the runway centerline:
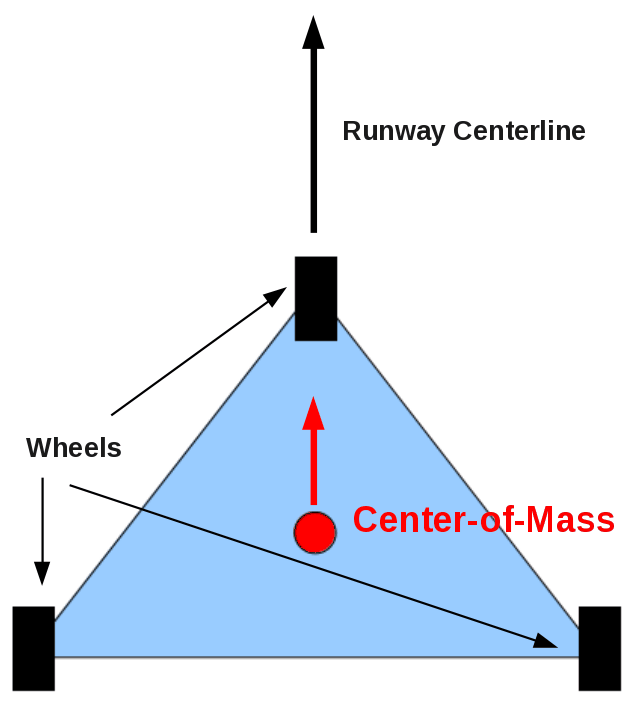
Figure 2: A tricycle-geared airplane, represented by a triangle, heading straight down the runway. The velocity of the center-of-mass (red circle) is pointing (red arrow) straight down the runway centerline. The three wheels are also parallel to the center-of-mass velocity vector, and will tend to produce no “yaw” about the center of mass.
Note that the center-of-mass of the tricycle wheeled aircraft is located forward of the fixed pair of main gear, and aft of the movable nosewheel. The center-of-mass is moving parallel to the runway centerline, and the axis of the aircraft (imagine where the fuselage would be) lies along this same line. The left-right symmetry of this arrangement insures that the passengers are in for a smooth and steady ride.
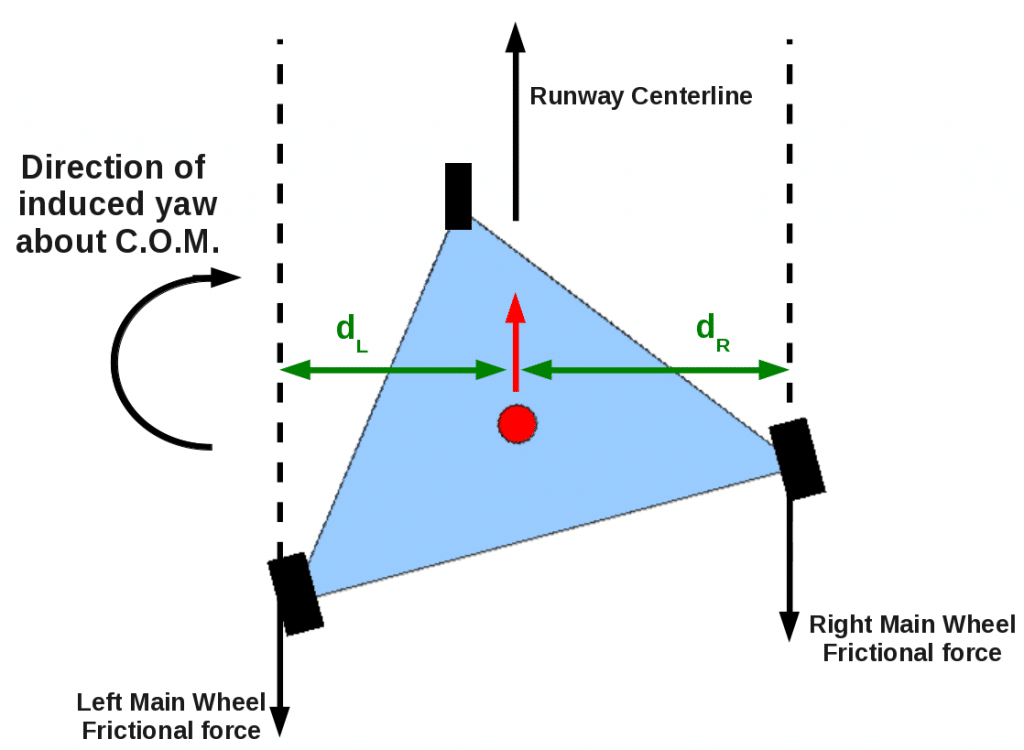
Figure 3: The same tricycle-geared airplane, its center of mass still moving in a direction parallel to the runway centerline. Now the airplane itself is at an angle to the direction of motion, as indicated by the nosewheel’s deflection to the left. The nosewheel, which is free to rotate, will still orient itself to roll parallel to the runway centerline. However, the fixed left- and right-main gear now experience an additional frictional force opposite the direction that the center-of-mass is moving. Note that the lever arm d_R of the right main gear is longer that the lever arm d_L of the left gear. This imbalance will produce a clockwise rotation about the center of mass, straightening out the tricycle-geared aircraft.
But consider what happens if the axis of the aircraft happens to be not aligned with the direction the center-of-mass wants to go (Figure 3). Perhaps there was a slight crosswind on landing, and the pilot had to crab the aircraft in order to get the center-of-mass moving parallel the runway centerline. Now when the wheels touch, the more-or-less freely rotating nosewheel will orient itself so as to roll straight down the runway. But the fixed main gear will meet the runway at an angle and experience a frictional force, directed opposite the direction of motion of the center-of-mass.
Because we are driving a tricycle wheel, however, a happy accident occurs. The two frictional forces, while equal in magnitude, happen at a different perpendicular distance (“lever arm”) from the line of motion of the center-of-mass. The greater lever arm d_R will produce a greater yaw-inducing torque about the center of mass and the plane will rotate clockwise, thus straightening itself out.
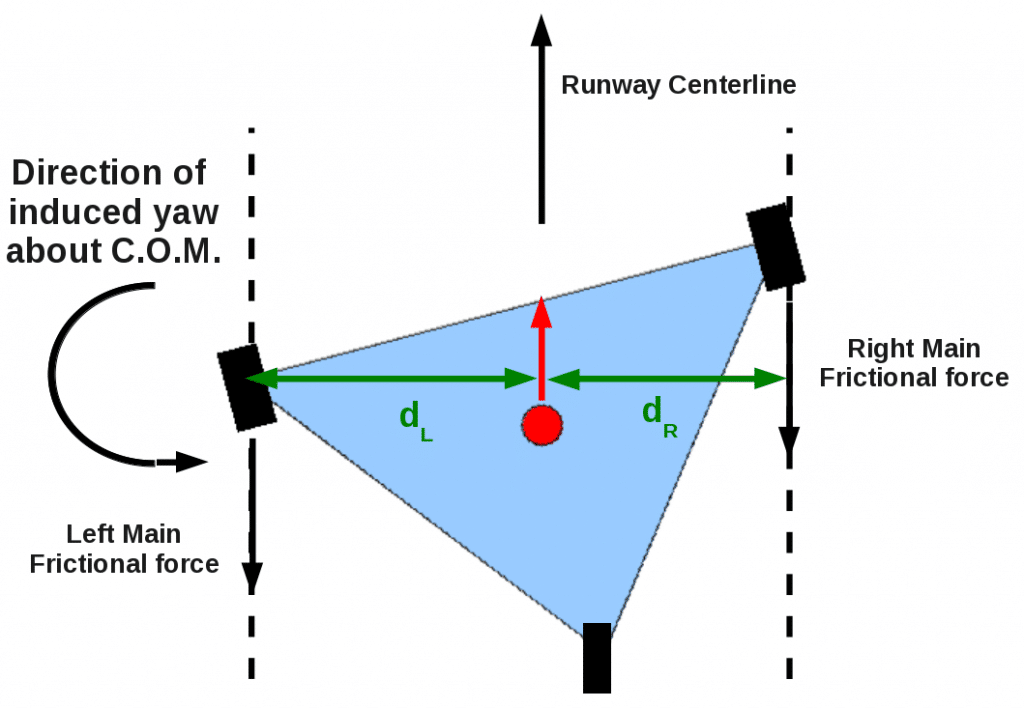
Figure 4: Now we consider a tailwheel (or “conventional geared”) aircraft. Tts center of mass is still moving in a direction parallel to the runway centerline. The tailwheel is off center, deflected to the right in this view and rotated so it still rolls parallel to the runway centerline. Again, the fixed left- and right-main gear now experience an additional frictional force opposite the direction that the center-of-mass is moving. Note that the lever arm d_L of the left main gear is longer that the lever arm d_R of the right gear. This imbalance will produce a counterclockwise rotation about the center-of-mass, and the aircraft will tend to rotate further from the centered position. If this rotation is not checked soon, a ground loop will develop.
You can probably already figure out what’s going to happen with a crabbed taildragger (Figure 4), with the center-of-mass located behind the fixed main gear. Now, the greater lever arm d_L belongs to the left main wheel. So the yaw-inducing torque is in the counterclockwise direction. And if the axis of the plane starts out misaligned with the direction the center-of-mass is moving the misalignment will tend to increase in magnitude. If the pilot does not take corrective action soon, a ground loop is looming!
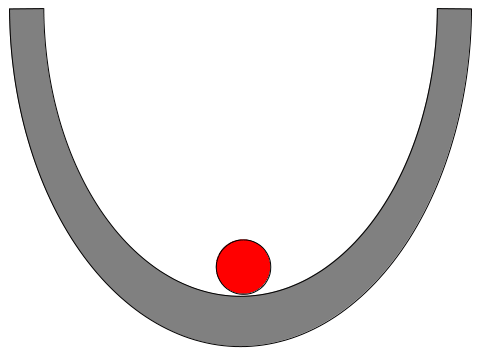
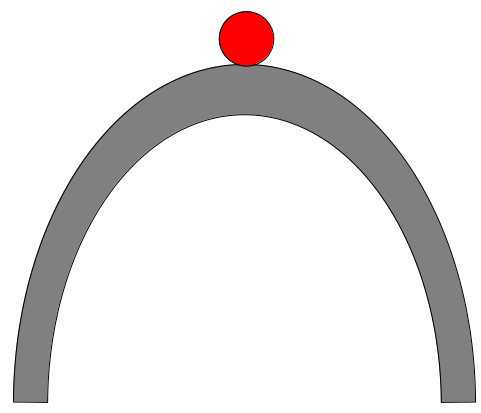
Figure 5: Left: The state of the red ball located at the bottom of the bowl is an example of “stable equilibrium”. The ball is experiencing no net force, but the response to a small nudge to either side will be a restoring force pushing the ball back to the equilibrium position. Right: Here, the red ball is in a state of “unstable equilibrium”. It is experiencing no net force, but a small nudge to either side will result in the ball accelerating away from the equilibrium position.
The performance during the landing roll of tricycles and taildraggers is an excellent illustration of stable and unstable equilibrium. As shown in Figure 5, an object in stable equilibrium “wants” to continue in its present state and any small perturbation will be countered by a force which tends to restore the equilibrium state. An object in unstable equilibrium will stay put as long as it is not perturbed, but the perturbations will tend to produce a runaway effect wherein the object flees the equilibrium position.
In writing this article, I have aimed to give some insight into the physics problem confronting a pilot transitioning from tricycle to tailwheel aircraft. I know that there’s a big gulf between simply knowing the physics, and training yourself to develop the required muscle memory to fly successfully. (Otherwise all physicists would be champions at billiards.) But hopefully, some perspective tailwheel pilot will find this as a useful mental picture while that muscle memory is developing.















I don’t think you really have the lever arm depicted properly.